Mathematik
Mathe-Rätsel
Satz-Fundus zur Elementargeometrie
(nach Prof. Dr. H. Möller, ehemals Universität Münster)
Dieser Fundus an elementaren Sätzen der Geometrie wurde von meinem Mathematik-Professor a.D. für Didaktik in Münster aufgestellt. Ich habe in Anlehnung seiner Ausführungen grundlegende Teile auf meiner Homepage zur Veröffentlichung aufgelistet und mit einer jeweilig erklärenden Grafik ergänzt.
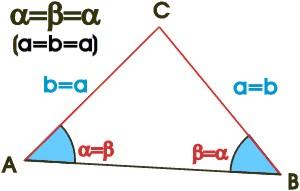
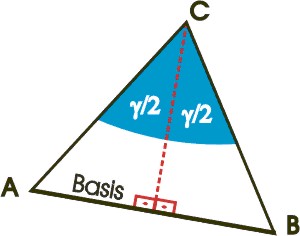
Basiswinkelsatz:
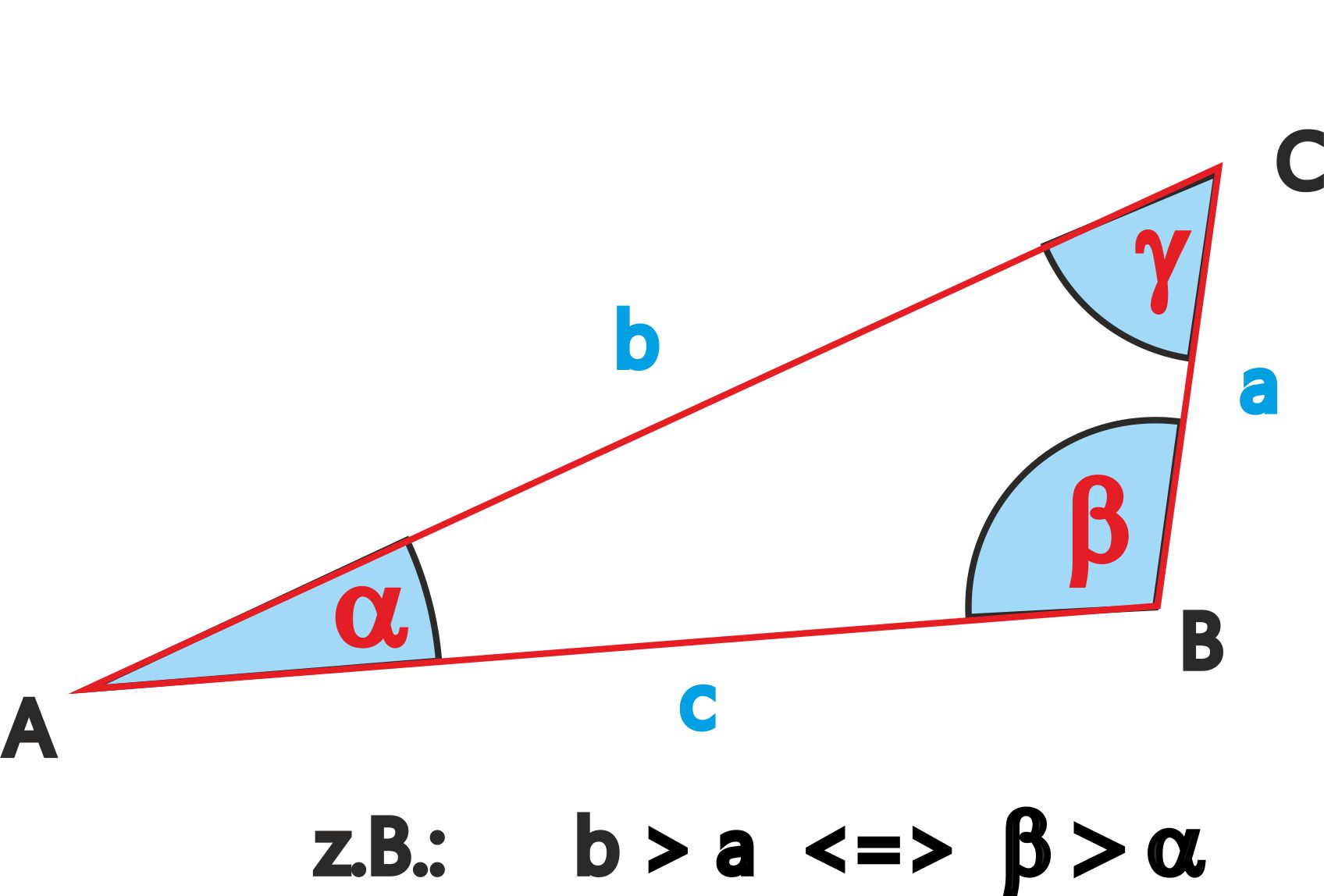
Dreieckseitensatz:
Kongruenzsatz:
Zwei Dreiecke sind kongruent, wenn eine der folgenden Übereinstimmungen vorliegt:
i) Die „Länge“ aller drei Seiten (SSS).
ii) Die Länge von zwei Seiten und die „Größe“ des von diesen eingeschlossenen Winkel (SWS).
iii) Die Länge von zwei Seiten und die Größe des Winkels, der der längeren Seite gegenüberliegt (WsS).
iv) Die Länge einer Seite und entweder die Größe der beiden „anliegenden“ Winkel (WSW) oder die Größe des gegenüberliegenden und eines anliegenden Winkels (SWW).
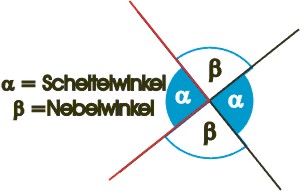
Winkelsatz:
Parallelensatz:

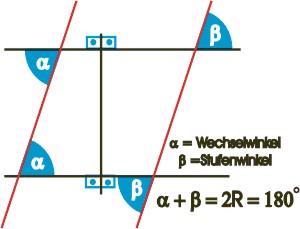
Je zwei Stufen- oder Wechselwinkel an geschnittenen Parallelen sind paarweise gleich; entgegengesetzte Winkel ergänzen sich zu 2R (=180°).
Werden zwei Geraden von einer dritten Geraden geschnitten und sind je zwei Stufen- bzw. Wechselwinkel einander gleich oder ergänzen sich je zwei entgegengesetzte Winkel zu 2R, so sind die geschnittenen Geraden parallel.
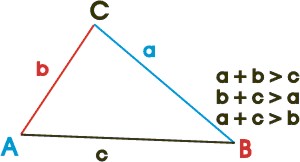
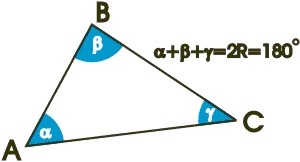
Seitensummensatz:
Innenwinkelsatz:
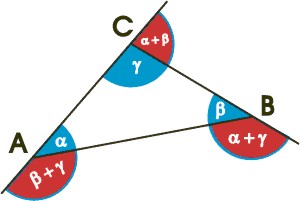
Aussenwinkelsatz:
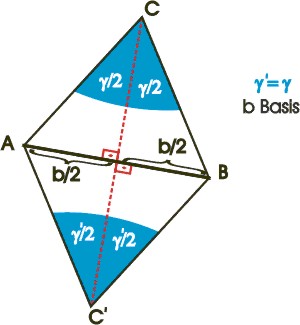
Drachensatz:
Gleichschenkelsatz:
Mittelsenkrechtensatz:
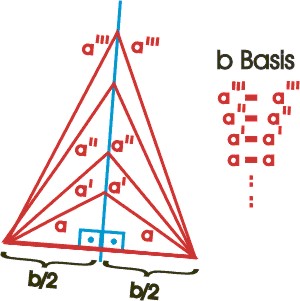
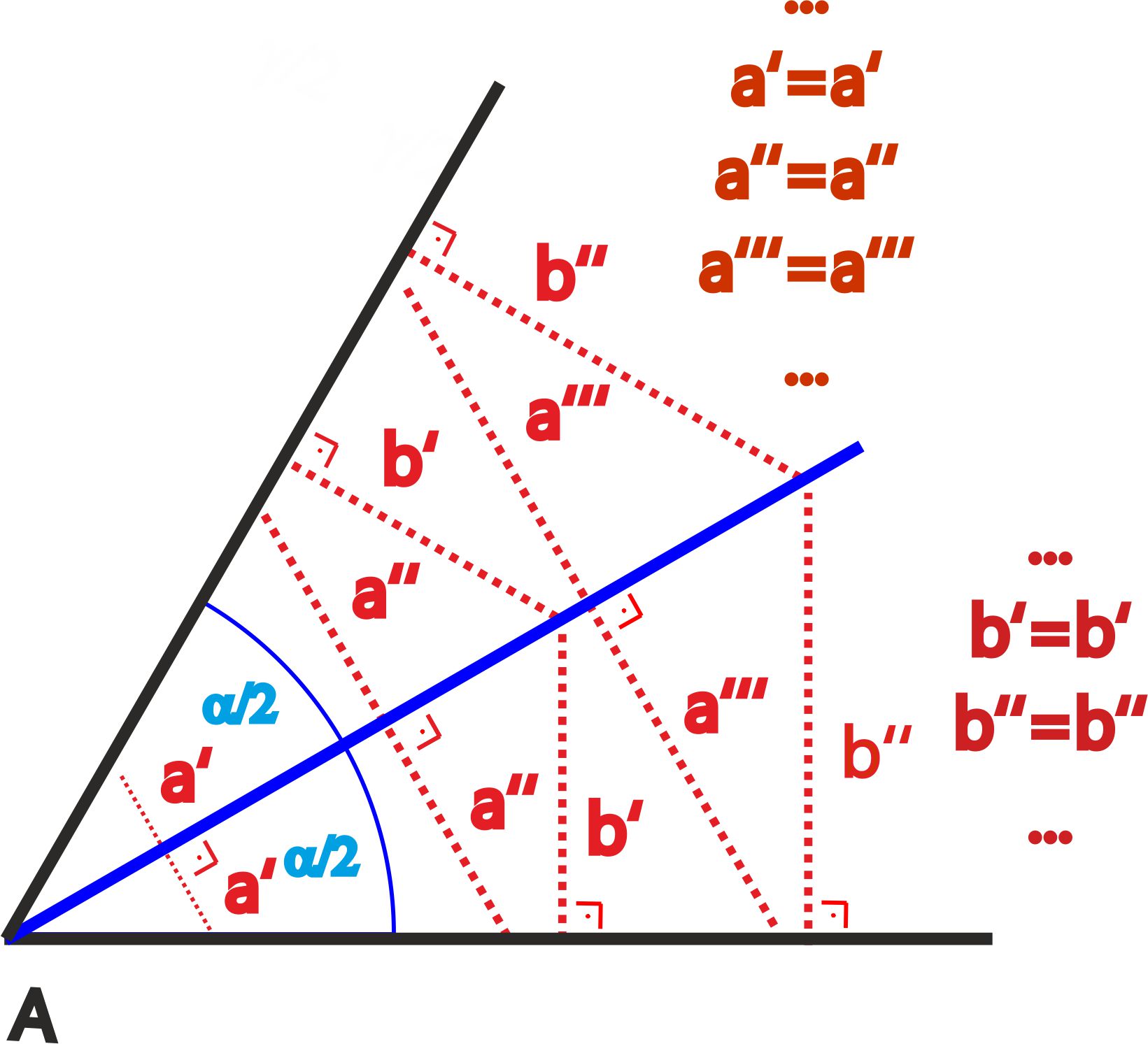
Winkelhalbierendensatz:
Parallelogrammsatz:
Das "Parallelogramm" wird durch jede seiner "Diagonalen" in zwei kongruente Dreiecke zerlegt, und die Diagonalen halbieren sich gegenseitig.
Im Parallelogramm sind die "Gegenseiten" und die "Gegenwinkel" gleich; die einer Seite anliegenden Winkel betragen 2R.
Ein "Viereck" ist ein Parallelogramm, wenn die Gegenseiten oder die gegenüberliegenden Winkel gleich sind oder wenn sich die Diagonalen gegenseitig halbieren oder wenn ein Paar Gegenseiten gleich und parallel sind.
Es ist genau dann ein "Rhombus", wenn die Diagonalen senkrecht aufeinander stehen oder wenn die Diagonalen die Winkel halbieren. Genau dann ist es ein „Rechteck“, wenn die Diagonalen gleich lang sind. Es ist genau dann ein „Quadrat“, wenn die Diagonalen senkrecht aufeinander stehen und gleich lang sind.
Trapezsatz:

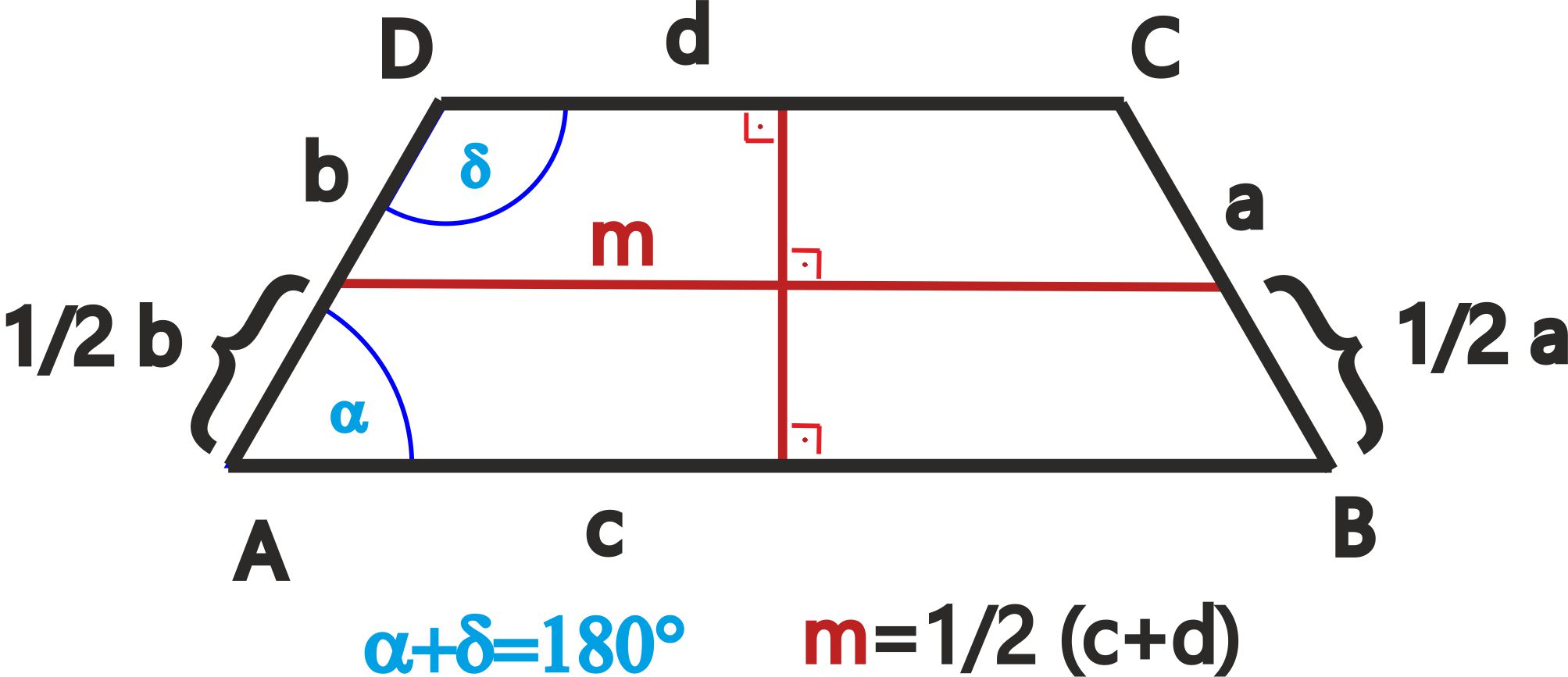
Im "Trapez" betragen die einem Schenkel anliegenden Winkel zusammen 2R.
Die "Grundlinienparallele" durch die Mitte eines Schenkels eines Trapezes halbiert den anderen Schenkel.
Die Verbindungslinie der Mitten der Schenkel eines Trapezes läuft den Grundlinien parallel.
Die "Mittellinie" einen Trapezes ist gleich der halben Summe der beiden Grundlinien.
Seitenmittensatz:
Zieht man durch die Mitte einer Dreiecksseite die Parallele
zu einer zweiten Seite, so halbiert diese die dritte Seite.
Die Verbindungslinie der Mitten zweier Dreiecksseiten läuft der dritten Seite parallel
und ist halb so lang wie diese.
Seitenhalbierendensatz:
Der Schnittpunkt von zwei "Seitenhalbierenden" eines Dreiecks teilt jede
der beiden Seitenhalbierenden im Verhältnis 2:1.
Die drei Seitenhalbierenden eines Dreiecks schneiden sich in einem Punkt (dem
"Schwerpunkt").
Sehnensatz:
Das vom "Mittelpunkt" eines "Kreises" auf eine "Sehne" gefällte
Lot halbiert den "Mittelpunktswinkel", die Sehne und den "Bogen".
Gleiche Sehnen haben gleichen Abstand vom Mittelpunkt.
Zu gleichen Sehnen gehören gleiche Mittelpunktswinkel und gleiche Bogen.
Der Mittelpunkt eines Kreises, der eine Strecke als Sehne hat, liegt auf der Mittel-
senkrechten der gegebenen Strecke.
Haben zwei Kreise eine Sehne gemeinsam, so steht diese auf der Verbindungsstrecke
der Mittelpunkte senkrecht.