SODUKO

Ein ausgesprochen forderndes Zahlenrätsel aus Japan ist Sudoku. Hierbei geht es nicht um das Rechnen mit Zahlen, sondern eher um die Möglichkeiten der Kombinationen. Je nach Menge und Zusammensetzung der Lücken auf der Vorlage gibt eine Menge von unterschiedlichen Schwierigkeitsgeraden. So gibt es meist zwei Möglichkeiten: Entweder man kommt nicht wieder davon los oder man verzweifelt an der Aufgabe...
weitere Infos zu Sodukos

Streichholzrästel

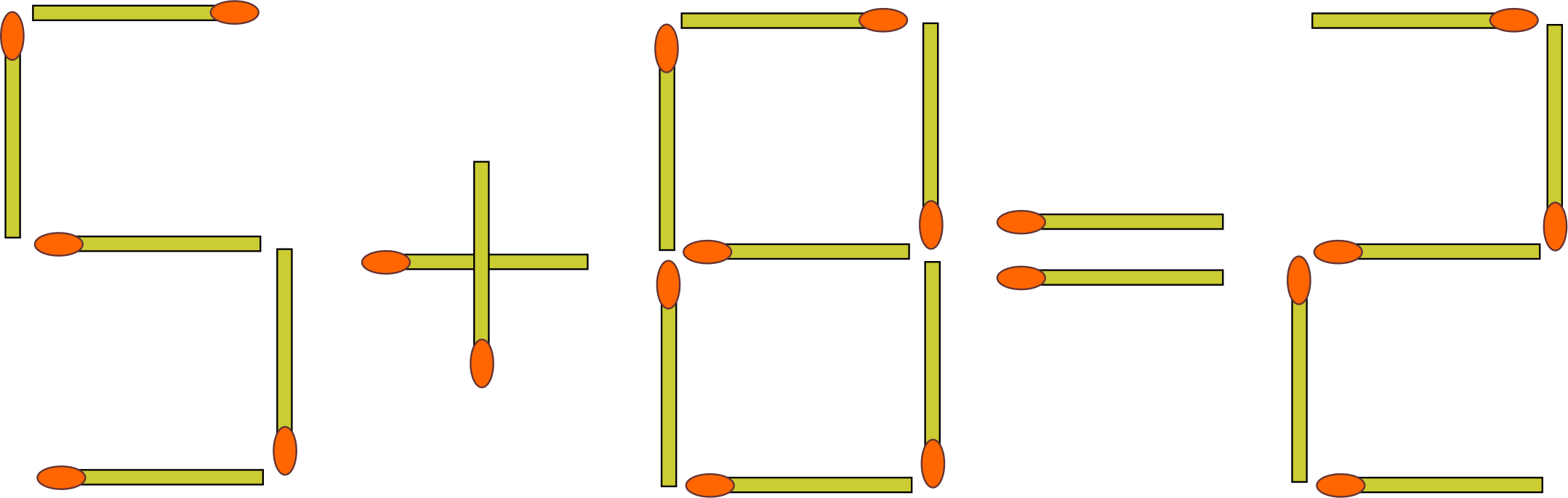
Es gibt unzählige Rästel, die sich einfach mit ein paar Streichhölzern legen lassen. Und genauso verblüffend ist es manchmal, wie sich durch einfaches Umlegen zum Beispiel von nur einem Streichholz sich ganze neue Zusammenhänge ergeben. Versuchen Sie doch einfach mal, das folgende Rästel zu entswchlüsseln:

Korrigieren Sie die Gleichung, indem Sie nur zwei Streichhölzer verlegen!

Geometriefundus

Die elementaren Sätze zur Geometrie sind manchmal simpel, manchmal schon schwieriger nachzuvollziehen. Aber es ist immer wieder interessant, wie alles zusammenhängt! Hier ein Beispiel...

Gleichschenkelsatz:

Die Verbindungslinie der Spitze eines gleichschenkeligen Dreiecks mit der Mitte der Basis halbiert den Winkel an der Spitze und steht senkrecht auf der Basis.
Dies gilt ebenso für die Mittelsenkrechte der Basis und dem Lot der Spitze.